セーブデータのロード
定義から、電源投入時の乱数位置は常に0だが、セーブデータをロードして操作可能になるまでに数百個の乱数が消費される。このとき、同一のデータでも、ロードを複数回試すと、操作可能になった時点での乱数位置が完全には一定しない。"セロビ台地/街道の休息所"でセーブしたデータで試したところ、乱数位置はおよそ570±10の範囲内だった。未検証だが、この挙動は本体の型番によって異なる可能性がある。なお、この調査に使用したPS2はSCPH-70000。
A系列の乱数を消費しない行動
- メニューの開閉、装備の変更、バトルメンバーの入れ替え、ライセンスの取得を行っても、いずれもA系列の乱数を消費しない。
- ブラナ、ボキャル、デスペルの各魔法は、実行しても乱数を一つも消費しない。また、(試した限りの)全てのアクションは、チャージ完了前に実行を中断すると乱数を消費しない。一方、バトルアルティマニアによれば、チャージタイムの算出には乱数が使われている。従って、アルティマニアの記述が正しければ、チャージタイムの決定に際して系列A以外の乱数が用いられていることになる。
- キャラクターは、銃で攻撃するとき、掛け声を発することがある。掛け声には複数の種類があり、どの掛け声を発するかはランダムに選ばれているように見える(ただし、同じ掛け声が二度連続で発せられることはないようだ)。一方、銃での攻撃に際して消費されるA系列の八個の乱数は全て用途が判明しており、掛け声の決定には別の系統の乱数が使われていると推測される。
興味のある人のために、系列A以外に見つかっている二つの擬似乱数生成器について分かっていることを書いておく。どちらの生成器も線形合同法を使っている。線形合同法の漸化式を「xn = (xn-1 * a + b) % m」と書くことにすると、一方は(a, b, m) = (6364136223846793005, 1, 264)で、各項xnに対して⌊xn / 232⌋ % 231を出力とする。初期値はおそらく1。もう一方は(a, b, m) = (75, 0, 231-1)で、各項をそのまま出力する。初期値はおそらく305420679。
応用例
乱数位置の特定
プレイ中、何らかの方法でその時点の乱数位置を具体的に特定することができれば、乱数位置を意図的に調整することで、その後の乱数の出方をある程度制御することができる。例えば、乱数位置を100個進めたいと思ったなら、自分に向けて銃を12回撃ち(死なないように属性吸収などの準備を講じた上で)、その後ケアルを4回唱えれば良い。
乱数位置の推定には、ダメージ量や回復量の数値を使うのが手軽だろう。乱数系列Aは完全に計算で求まるので、各乱数位置に対して予め例えば「その位置でケアルダを唱えたときの回復量」を計算して表にしておき、実際に2~3回ケアルダを唱えてみてその回復量の並びを表から探す。「全ての乱数位置」を網羅した表を作るのはもちろん不可能だが、実際には10万未満の乱数位置の範囲で表を作れば大抵事足りる。
考え方としてはこの作業は単純だが、手で計算して表を作るのは計算量が膨大なので現実的でない。この作業を補助する簡単なJavaScriptツールを同梱したので、興味があれば試して欲しい。
5hits法の原理
5hits法とは、もともとIZJSで発見された手法で、大まかに以下の手順に従うことでトレジャーからレアアイテムを高確率で得ることができるというものである。
- トレジャーの近くでセーブし、ハードウェアリセットをする。
- ロードし、目標のトレジャーがPOPするまでゾーンチェンジを繰り返す。ただし、ある程度繰り返してもPOPしない場合は最初からやり直す。
- 自分を繰り返し殴る。このとき、ガードが発生しないように盾は外すか、カメオのベルトを装備する。
- 5 hitsの連撃が発生したら、ダイヤの腕輪を装備して目的のトレジャーを開ける。
- 条件として、トレジャーを開けるまで敵に攻撃されてはいけない。
結論から言うと、この手法は、トレジャーを開ける時点での乱数位置を1445に固定することで機能している。この付近の系列Aは次のようになっている。
1444: 2510889783 1445: 1861786791 1446: 1379767799 1447: 80686868
位置1445と1446の値は下二桁がそれぞれ91と99で、どちらも大きい。これは、かなり確度の大きな%判定でも失敗するということである。実際、乱数位置が1445の状態でトレジャーを開けた場合、ギル判定と非レア判定はどちらも最大確度90なので確実に失敗し、結果としてレアアイテムが手に入る。なお、IZJSの透明武具は非レア判定の確度が95であるようだが、比較対象は99なのでやはり失敗する。
5 hitsの連撃自体は、乱数位置が1388のときに素手で攻撃すると発生する。
1387: 382760416 1388: 2267807233 ここで攻撃; ノックバック確率計算1 1389: 1886692943 ノックバック確率計算2 1390: 2131861130 ノックバック判定 1391: 2952945076 (不明) 1392: 2341692401 連撃判定(確度3) → 成功 1393: 3404601602 連撃回数増加判定(確度8) → 成功 1394: 2203834536 連撃回数増加判定(確度8) → 失敗 1395: 961042754 連撃回数増加判定(確度8) → 失敗 1396: 2005317402 連撃回数増加判定(確度8) → 成功 1397: 2981387111 連撃回数増加判定(確度8) → 失敗 1398: 2833431843 連撃回数増加判定(確度8) → 失敗 1399: 3060953428 連撃回数増加判定(確度8) → 失敗 1400: 3953158966 連撃回数増加判定(確度8) → 失敗 1401: 3263761202 連撃回数増加判定(確度8) → 成功 1402: 161153939 連撃回数増加判定(確度8) → 失敗 1403: 1977869617 連撃回数増加判定(確度8) → 失敗; 5 hitsの連撃発生 1404: 3808337799 盾ガード判定(確度0) → 失敗 1405: 3799551709 ...(以下略)...
5 hitsの連撃によって57個の乱数が消費されるので、連撃後の乱数位置はちょうど1445になる。
なお、連撃が発生しない場合、自分を殴る毎に乱数位置は10ずつ進む。そのため、位置1388に到達して5 hitsを発動させるためには、乱数位置の一の位がちょうど8である状態で自分を殴り始めなければいけないように思える。しかし、実際には、一の位は0か1でもよいことがある。一の位が0なら、位置1070で4 hitsの連撃が発生し、連撃終了後には位置が1118になるので、あと27回の自打で1388に達する。一の位が1の場合、位置751で3 hitsの連撃が発生し、乱数が39個消費されて位置が790になる。これもあと26回の自打で1070に達する。
このように、乱数位置1388は自打の繰り返しによって比較的到達しやすく、滅多にない5 hitsという連撃を発生させ、しかも連撃直後の乱数位置がトレジャーの開封に非常に適しているという、良い性質を併せ持った稀有な位置であり、5hits法はこの特殊な性質をうまく利用している。
"セロビ台地/交差ヶ原"のトレジャーPOP法則
乱数の絡む事象がどのような法則に基づいて決定されるのか調査する手順を、具体例を通して紹介する。例として、"セロビ台地/交差ヶ原"内の各トレジャーが出現するかどうかがどのように決定されるか調べる。
シナリオアルティマニアのp.122によると、トレジャーが出現するかどうかはそのゾーンを訪れたときに決定される。そこで、まず、交差ヶ原に進入するときにいくつの乱数が消費されるか調べてみる。
まず、リセット後、街道の休息所のセーブデータをロードし、銃のダメージを使って乱数位置を特定する。その後交差ヶ原に入り、再び乱数位置を特定、ゾーン進入直後の乱数位置を逆算する。二つの乱数位置の差を取ることで、交差ヶ原に進入したとき16個の乱数が消費されたことが分かった。
街道の休息所に戻り、もう一度同じ手順で進入時の乱数消費を計る。すると、今度は6個しか乱数が消費されなかった。これは、トレジャーの再出現の条件を満たしていないためにトレジャーの出現判定が省略されたからだと考えられる。アルティマニアによると交差ヶ原内のトレジャー出現位置は10箇所であり、最初の16個の乱数消費のうち10個がトレジャーの出現判定に費やされていたと考えると辻褄が合う。
では、消費された16個の乱数のうちどれがどのトレジャーの出現判定に利用されたのか考える。アルティマニアによると10箇所のトレジャーの出現率は全て50%となっている。そこで、ひとまずトレジャーの出現判定が確度50の%判定によって行われていると仮定してみる。消費された16個の乱数について、その位置で確度50の%判定を行った場合の成否を並べると、次のようになった。
n y n n n n n y n y y n n y y n (yは成功、nは失敗)
次に、交差ヶ原を実際に回って、どの位置のトレジャーが出現しているかを確認する。出現していたトレジャーは4つで、具体的には、アルティマニアのトレジャー番号を使って呼ぶと、55, 57, 59, 60だった。
16個の乱数消費のうち、トレジャーの出現判定に使われた乱数位置は連続していると仮定してみる。つまり、トレジャーの出現判定の間に無関係な乱数消費がないと仮定する。先の16個の%判定の合否列のうち、長さ10で、そのうちちょうど4つが成功している部分列は二通りしかない。
n[y n n n n n y n y y]n n y y n および、 n y n n[n n n y n y y n n y]y n
ここまでの仮定が正しければ、このうちどちらかがトレジャー判定の部分に対応している可能性が高い。
今あるデータだけではこれ以上のことは何も言えそうにないので、一旦セーブ/リセットして同様のデータを別ケースについて集める。これを繰り返して計5回分のデータを集めた。
0: n y n n n n n y n y y n n y y n 出現: 55, 57, 59, 60 (これが最初のデータ) 1: n y n y n y n y n n n y n y y n y 出現: 52, 53, 58, 59 2: y n y n y n n n y n y y n y n n y 出現: 51, 55, 57, 59, 60 3: n y n n y y n n y n y n y n y n n 出現: 51, 52, 57, 60 4: y n y y n n n n y y n y n n y y 出現: 51, 53, 56, 60
まず予想外のこととして、交差ヶ原進入時の乱数消費が16個でなく17個である場合があった。このケースでは、トレジャーの出現判定部分の前か後かのどちらかで、追加の乱数消費があったと仮定することにする。
以上の仮定のもとで、結果を矛盾なく説明できる乱数の使い方が一つだけあることが分かった(このチェックにはコンピュータを使ったが、人力でもできないことはないと思う)。具体的には以下の通り。
- 乱数を1個または2個消費する(使途不明、1個か2個かの条件も不明)。
- 乱数を10個消費して、一個ずつトレジャーの出現判定に使う。判定の順序は、55, 53, 51, 52, 54, 58, 57, 56, 60, 59。
- 乱数を5個消費する。rémy lachaudによるとこれはトラップの種別決定に用いられる(一箇所につき一個)。
これで、計16個または17個の乱数を消費することになる。
以上で、交差ヶ原のトレジャーPOP法則について仮説を立てることができたので、次はこれを検証する。もう一度リセットして実際に試したところ、大体仮説どおりのPOP状況になっていた(本来はもっとまじめに検証すべきなのだろうが、単純作業の繰り返しにいい加減飽きていたので適当)。最後の締めくくりとして、乱数位置を調整してリボンのトレジャーをPOPさせ、実際にリボンを入手して終了。
交差ヶ原の地図に、各トレジャーの出現判定の順序を書き込むと次のようになる。
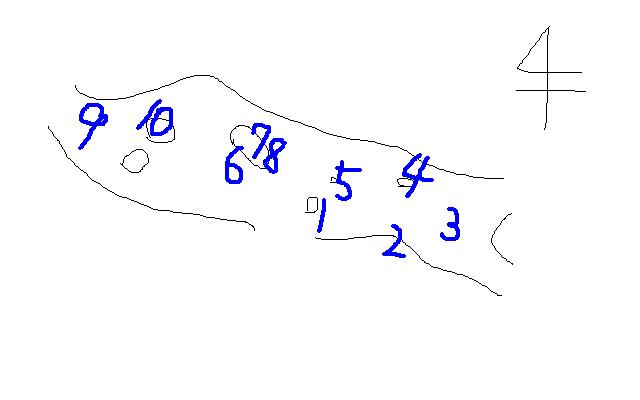
分かっていないこと
現状では分かっていることの方が少ないが、すぐ思いつく未調査点は以下。
- バトルアルティマニアp.79によると、くらやみ状態ではガード率とパリィ率が二倍の補正を受ける。しかし、実際に実行者をくらやみにして素手での攻撃を試すと、盾ガード判定、武器ガード判定、パリィ判定の三つの確度を単純に二倍にしただけでは結果を正しく予測できないようである。
- "セロビ台地/交差ヶ原"に進入したときの乱数の消費個数が一定しない原因。天候が関係しているような気がするが未調査。
- モンスターのドロップアイテムについて。
- 街中での乱数消費。